Bei der Berechnung von Wälzlagern wird meist von idealen Nenngeometrien ausgegangen. Allerdings unterliegen reale Bauteile und -gruppen stets statistisch verteilten Geometrieabweichungen, die sich aus dem Fertigungs- und Montageprozess ergeben. Infolgedessen kommt es zu Veränderungen der lagerinternen geometrischen Verhältnisse, welche sich auf die Eigenschaften des Lagers – beispielsweise auf die Lebensdauer – auswirken. Die Software FVA-Workbench bietet Anwenderinnen und Anwendern die Möglichkeit, diese geometrischen Abweichungen bei der Lagerberechnung zu berücksichtigen und so die Zuverlässigkeit der erhaltenen Ergebnisse zu erhöhen.
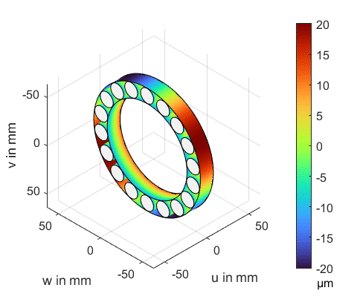
Laufbahnen eines Zylinderrollenlagers mit kegeliger Formabweichung der Innenringlaufbahn und Ovalisierung der Außenringlaufbahn
1 Problemstellung
Wälzlager sind unverzichtbare Komponenten in allen Bereichen des heutigen Maschinenbaus, da sie eine präzise, reibungsarme und gleichzeitig kostengünstige Lagerung rotierender Bauteile ermöglichen. Die Berechnung von Wälzlagern erfolgt heute i. d. R. nach ISO/TS 16281. Dabei wird regelmäßig davon ausgegangen, dass die realen Laufbahnen eine idealisierte Geometrie aufweisen und keine Fluchtungsfehler der Lagerachsen vorliegen.
In der Praxis ist diese Idealsituation jedoch nie vollständig erreichbar. Reale Fertigungs- und Montageprozesse führen stets zu geometrischen Abweichungen, wobei deren Ausprägung einer statistischen Verteilung folgt [2]. Darüber hinaus können die im Betrieb wirkenden Belastungen Verformungen hervorrufen, welche das Betriebsverhalten der Lager beeinflussen. FINGERLE [3] hat bspw. gezeigt, dass die an Planetenrädern wirksamen Zahneingriffskräfte eine Ovalisierung des Radkörpers verursachen. Im Vergleich mit einem ideal steifen Rad führen diese entsprechend der vorliegenden Randbedingungen zu einer Reduzierung oder Erhöhung der Lagerlebensdauer.
Die Integration geometrischer Abweichungen und ihrer statistisch verteilten Ausprägungen bei der Berechnung von Wälzlagern bedeutet somit eine genauere Abbildung der Realität und führt daher zu einer Verbesserung der Ergebnisqualität.
Die Software FVA-Workbench [4] erlaubt es der Anwenderin und dem Anwender, Wälzlagerungen unter Berücksichtigung von Form- und Lageabweichungen auszulegen. Über eine Skripting-Schnittstelle besteht dabei auch die Option, benutzerdefinierte Routinen einzubinden. Im Folgenden wird gezeigt, wie diese Möglichkeiten genutzt werden können, um eine Lagerberechnung unter Einbeziehung statistisch verteilter geometrischer Abweichungen durchzuführen.
2 Berücksichtigung geometrischer Abweichungen bei der Wälzlagerauslegung
In der FVA-Workbench können Getriebesysteme modelliert, parametrisiert und berechnet werden. Bei der Modellierung des Gesamtsystems ist dabei auch der Import einer STP-Datei des Gehäuses möglich, welche anschließend mithilfe eines einfachen Klick-Workflows an die Lageraußenringe gekoppelt werden kann. Dies ermöglicht die Berechnung der Steifigkeitsmatrix und die Bestimmung der Ersatzsteifigkeit nach GUYAN [5] ohne Verwendung einer externen FE-Software.
Neben der Verwendung von Lagerdaten nach Herstellerangaben (z. B. aus Wälzlagerkatalogen) ist auch eine direkte Eingabe der Wälzlagergeometrie möglich. Dies schließt die Profilierung der Wälzkörper und Laufbahnen mit ein. Auf diesem Weg lassen sich Formabweichungen sehr einfach berücksichtigen.
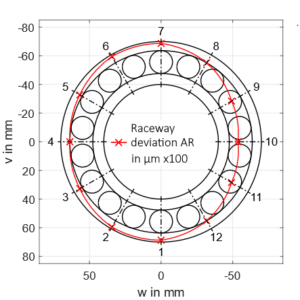
01: Exemplarische Formabweichung der Außenringlaufbahn entlang des Umfangs (AR ≙ Außenring), Darstellung hundertfach überhöht
Die Abweichungen auf der Außenringlaufbahn können als radiale Abweichungen von der idealen Kreisform definiert werden. Damit kann zum Beispiel eine Ovalisierung des Lageraußenrings vorgegeben werden.
In Bild 01 wird eine beispielhafte Formabweichung des Außenrings gezeigt. Zur Verdeutlichung ist die Formabweichung hundertfach überhöht dargestellt.
Für Wälzlager mit Linienkontakt können beliebige Profilierungen in axialer Richtung für die Wälzkörper am Innen- und Außenring definiert werden.
In der Regel werden herstellerseitig gezielt ausgelegte Profilfunktionen zur Verbesserung der Lebensdauer eingesetzt. Prinzipiell sind jedoch beliebige axiale Formabweichungen der Laufbahnen darstellbar.
In Bild 02 sind einige beispielhafte Abweichungen in axialer Richtung mit acht Stützpunkten grafisch dargestellt. Die Wälzkörper entsprechen dem Profilvorschlag nach DIN 26281 – mit einer balligen Formabweichung am Innenring und einer kegelförmigen Formabweichung am Außenring. Auch hier sind die Werte im Sinne der Sichtbarkeit hundertfach überhöht.
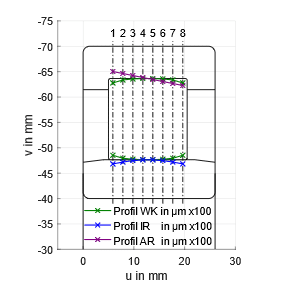
02: Exemplarische Formabweichungen in axialer Richtung (Profilierungen) an einem Zylinderrollenlager (WK ≙ Wälzkörper, IR ≙ Innenring, AR ≙ Außenring), Darstellung hundertfach überhöht
DIN 26281 schreibt für die Anwendung des Scheibenmodells die Unterteilung des Lagers in mindestens 30 axiale Scheiben vor. Die FVA-Workbench ermöglicht eine beliebige Auflösung, solange die Untergrenze nicht unterschritten wird. Um die gewünschte Profilierung im Scheibenmodell optimal abbilden zu können, empfiehlt es sich, die Anzahl der Stützpunkte der Profilierungen mindestens so groß zu wählen wie die Anzahl der Scheiben.
Am Außenring besteht somit auch die Möglichkeit einer additiven Überlagerung von Abweichungen in Längs- und Umfangsrichtung.

03: Ablauf der statistischen Toleranzanalyse bei der Wälz-lagerberechnung mit FVA Workbench
Neben derartigen Formabweichungen der Laufbahnen ist auch die Definition eines Versatzes sowie einer Schiefstellung des Gehäuselagersitzes möglich, welche durch je einen Wert für die Hoch- (v) und Querachse (w) beschrieben werden (zur Bezeichnung der Achsen s. Bild 04). Bei der Berechnung stellen diese Werte Randbedingungen dar, welche bei der Lösung des quasistatischen Gleichgewichts im System Welle-Lager-Gehäuse entsprechend berücksichtigt werden.
Um komplexe Prozesse in der FVA-Workbench zu automatisieren, bietet sich das Skripting-Modul [6] an. Mit einfachen Befehlen lassen sich zusätzliche Daten laden, Berechnungen ausführen und eigene Ausgabereports erstellen. Ausgabeformate können einfache Textdateien, übersichtlich aufbereitete HTML-Reports oder fertig konfigurierte Excel-Dateien sein.
Über das Skripting-Modul können z. B. zuvor generierte Samples geladen und der Reihe nach abgearbeitet werden. Ein Sample beschreibt in diesem Zusammenhang eine mögliche Konfiguration von Abweichungen, wie sie auch real auftreten können.
Der Ablauf der statistischen Toleranzanalyse im vorliegenden Beitrag ist in Bild 03 dargestellt. Die Berechnung wird in einer XML-Datei konfiguriert. Hier werden die Komponenten und die Form- und Lagetoleranzen definiert. Auf Basis dieser Eingabedatei werden die Samples dann automatisiert auf Basis der eingestellten Samplingstrategie (zufallsbasiert oder systematisch nach einem Versuchsplan) erstellt. Die Verarbeitung der Eingabedatei erfolgt über ein Matlab-Skript, welches die Geometriedaten der einzelnen Samples in einer Excel-Datei abspeichert, die von der FVA-Workbench gelesen werden kann. Zusätzlich benötigt diese als Input eine Modelldatei, an der die gewünschten Berechnungen durchgeführt werden.
Anschließend wird die FVA-Workbench über einen Kommandozeilenaufruf im Batch-Modus gestartet, welche dann die erzeugten Samples automatisiert abarbeitet und schließlich die Berechnungsergebnisse in einer Excel-Datei speichert.
Die statistische Analyse der Ergebnisse erfolgt anschließend mithilfe entsprechender Matlab-Skripte. Über eine entsprechende Funktion ist es auch möglich, für einzelne Samples einen Ergebnisreport in der FVA-Workbench zu generieren. Dieser wird im HTML-Format ausgegeben und beinhaltet detaillierte, grafisch aufbereitete Berechnungsergebnisse für die einzelnen Systemkomponenten (z.B. Wellenbiegung, Flankenpressung in Zahneingriffen oder Lebensdauer).
3 Berechunungsbeispiel
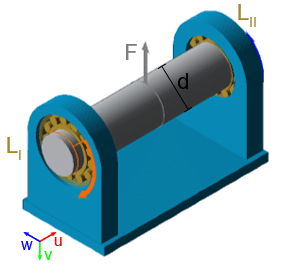
04: Systemmodell für die Berechnung
Im Folgenden wird der Ablauf anhand eines Beispiels demonstriert. Exemplarisch wird ein einfaches System, bestehend aus einem Gehäuse und einer darin in einer Fest-Los-Lagerung geführten Welle betrachtet, wobei in der Wellenmitte eine Radialkraft F angreift (s. Bild 04).
Die folgende Tabelle zeigt eine Übersicht der konstanten Berechnungsparameter:
| Parameter | Wert | Einheit |
|---|---|---|
| Gehäusematerial | EN-GJL-200 | – |
| Wellenmaterial | 16MnCr5 | – |
| Wellendurchmesser d | 90 | mm |
| Drehzahl | 2000 | 1/min |
| Radialkraft F | 66,4 | kN |
| Relative Lagerlast C/P | 5 | – |
| Lagerabstand | 356 | mm |
| Lagertyp LI | NU216 | – |
| Lagertyp LII | NUP216 | – |
| Lagerluftklasse | CN | – |
| Wälzkörperprofil | DIN 26281 | – |
| Temperatur Außenring | 70 | °C |
| Temperatur Innenring | 75 | °C |
| Temperatur Wälzkörper | 77 | °C |
| Schmierstoff | FVA3 | – |
| Temperatur Schmierstoff | 47 | °C |
Neben diesen unveränderlichen Parametern wird am Lager I eine variable Ovalisierung des Außenrings vorgegeben. Die Ovalisierung hat eine Amplitude zwischen 0 µm und 20 µm bei einem Phasenwinkel zwischen 0° und 360° – diese wird mithilfe der diskreten Fouriertransformation (DFT) modelliert. Weiterhin wird eine Kegeligkeit des Innenrings in einem Wertebereich von -5 bis 5 Winkelminuten (‘) simuliert.
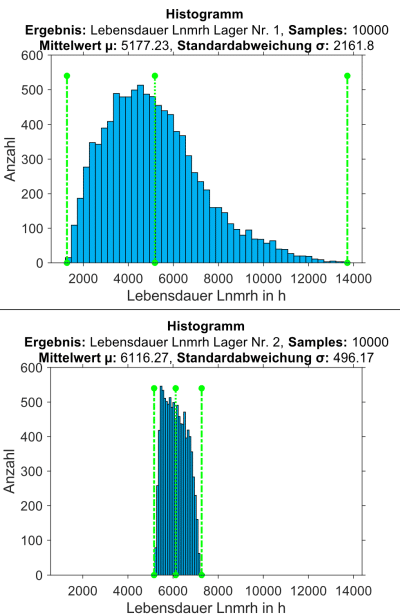
05: Histogramme Lebensdauern Lnmrh Lager I (oben) und Lager II (unten)
Die Ovalisierung wird in der FVA-Workbench als Formabweichung des Außenrings in Umfangsrichtung abgebildet (vgl. Bild 01), während die Kegelig-keit eine axiale Formabweichung des Innenrings darstellt (vgl. Bild 02). Des Weiteren wird für beide Lager die Variation der Lagerluft innerhalb der zulässigen Grenzwerte für die Klasse CN berücksichtigt. Im Fall des Lagertyps NU216 bzw. NUP216 entspricht dies nach DIN 620-4 [7] einem Intervall zwischen 40 und 75 µm. Dies wird in Form einer Durchmesseränderung am Außenring modelliert, welche jeweils zur Ovalisierung hinzuaddiert wird. Die konkreten Werte für jedes einzelne Sample werden durch Latin Hypercube Sampling („Versuchsplan“) ermittelt.
Es werden insgesamt 10000 Einzelfälle ausgewertet, wobei das Sampling der veränderlichen Werte nach einem Latin Hypercube Design (LHD) mit minimierter Korrelation der Variablen erfolgt. Durch diese Samplingstrategie wird eine bestmögliche Abdeckung des Parameterraums erreicht [8]. Die Berechnungsdauer auf einer Desktop-Workstation beträgt dabei knapp 90 Minuten.
In Bild 05 sind die Verteilungen der resultierenden modifizierten Referenzlebensdauern in Stunden (Lnmrh) nach DIN 26281 für beide Lager in Histogrammform dargestellt. Wie zu erkennen ist, ist die Streuung der Lebensdauern bei Lager I deutlich größer als im Fall von Lager II. Der Wertebereich für das Lager I erstreckt sich dabei zu beiden Seiten über den des Lagers II hinaus. Das heißt, es können sowohl höhere als auch niedrigere Lebensdauern als bei Lager II auftreten. Dies ist auf die definierten geometrischen Abweichungen am Lager I zurückzuführen, deren Effekte im Folgenden genauer analysiert werden.
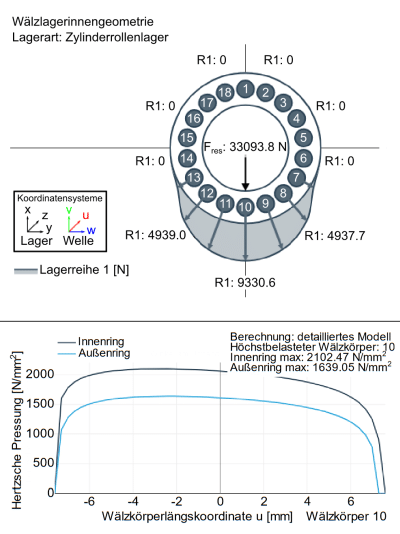
06: Wälzkörperlastaufteilung (oben) und axialer Pres-sungsverlauf am höchstbelasteten Wälzkörper (unten)
bei Median-Lebensdauer Lnmrh am Lager II
Als Referenz sind in Bild 06 für den Medianwert (6096 h) der Lebensdauer Lnmrh am Lager II – bei dem lediglich die Lagerluft innerhalb der Grenzen der Klasse CN variiert – die lagerinterne Lastaufteilung auf die Wälzkörper sowie die axialen Pressungsverläufe des höchstbelasteten Wälzkörpers (Nr. 10) für den Innen- und Außenringkontakt aus dem FVA-Workbench Ergebnisreport abgebildet. Die Berechnung von Einfederung und Pressungsverteilung der Lager erfolgt dabei nach TEUTSCH & SAUER [9]. Die Wälzkörper-Lastverteilung (oben) folgt dem typischen bogenförmigen Verlauf, während die Pressungen in axialer Richtung (unten) aufgrund der Wellenbiegung in negativer u-Richtung zunehmen. Zu beachten ist dabei, dass am Innenring aufgrund des nicht konformen Kontakts höhere HERTZ’sche Pressungen auftreten als am Außenring.
Im Vergleich hierzu zeigt Bild 07 für die Samples mit minimaler (links) bzw. maximaler Lebensdauer Lnmrh (rechts) des Lagers I eine Visualisierung der Laufbahngeometrien sowie der zugehörigen Wälzkörperlastverteilungen und der axialen Pressungsverläufe.
Wie zu erkennen ist, liegt in beiden Fällen eine deutliche Ovalisierung der Außenringlaufbahn vor. Beim Sample mit maximaler Lebensdauer beträgt deren Wert 18,06 µm. Die große Halbachse des Ovals ist parallel zur Last ausgerichtet. Die Innenringlaufbahn weist in diesem Fall eine Kegeligkeit mit einer negativen Steigung in u-Richtung auf. Der zugehörige Steigungswinkel beträgt -0,98 Winkelminuten.
Die Lebensdauer Lnmrh ist hier mit 13721 h mehr als doppelt so hoch wie der Medianwert bei Lager II (6096 h), was auf einen positiven Einfluss der geometrischen Abweichungen auf die lagerinternen Lastverhältnisse zurückzuführen ist. So bewirkt die Ovalisierung im Vergleich zu Lager II eine gleichmäßigere Lastverteilung auf die Wälzkörper und somit eine deutliche Reduzierung der Spitzenlast (vgl. Bild 06 oben und Bild 07 mittig rechts). Während am Lager II die maximale Wälzkörperlast 9330,60 N beträgt, liegt diese am Lager I im günstigsten Fall bei nur 6350,70 N.
Die Kegeligkeit am Innenring gleicht den Einfluss der Wellenbiegung aus. Infolgedessen ist der axiale Pressungsverlauf am Innenring nahezu symmetrisch zur Mittellinie und die maximale HERTZ’sche Pressung sinkt – auch aufgrund der reduzierten Wälzkörperlast – im Vergleich zum Lager II von 2102,47 MPa auf 1776,0 MPa (vgl. Bild 06 unten und Bild 07 unten rechts).
Im Fall des Samples mit minimaler Lebensdauer hingegen bewirken die geometrischen Abweichungen einen gegenteiligen Effekt, nämlich eine deutliche Verminderung der Lagerlebensdauer im Vergleich zum Medianwert am Lager II (1273 h gegenüber 6096 h). Auch hier ist die Außenringlaufbahn ovalisiert. Die Amplitude weist dabei mit 18,08 µm nahezu den gleichen Wert auf wie im Optimalfall zuvor. In diesem Fall jedoch liegt die große Halbachse quer zur Lastrichtung (vgl. Bild 07 oben links und rechts). Dies hat eine ungleichmäßigere Lastverteilung auf die Wälzkörper, d. h. eine weitere Erhöhung der Spitzenlast am höchstbelasteten Wälzkörper im Vergleich zu Lager II zur Folge (11298,30 N, vgl. Bild 07 mittig links ggü. 9330,60 N, vgl. Bild 06 oben).
Der Steigungswinkel der Kegeligkeit ist hier deutlich positiv (4,94′) und verstärkt daher den aus der Wellenbiegung resultierenden axialen Spannungsgradienten zusätzlich. Statt der im Optimalfall gleichmäßigen Lastverteilung in Umfangs- und Längsrichtung führen die höhere Wälzkörperspitzenlast und das axiale Spannungsgefälle zu einem ausgeprägten lokalen Beanspruchungsmaximum im Kantenbereich des höchstbelasteten Wälzkörpers (maximale HERTZ’sche Pressung 2626,07 MPa gegenüber 1776 MPa im Optimalfall bzw. 2102,47 MPa beim Lebensdauer-Median am Lager II, s. Bild 06 unten und Bild 07 unten). Infolgedessen sinkt hier auch die zu erwartende Lagerlebensdauer deutlich ab.
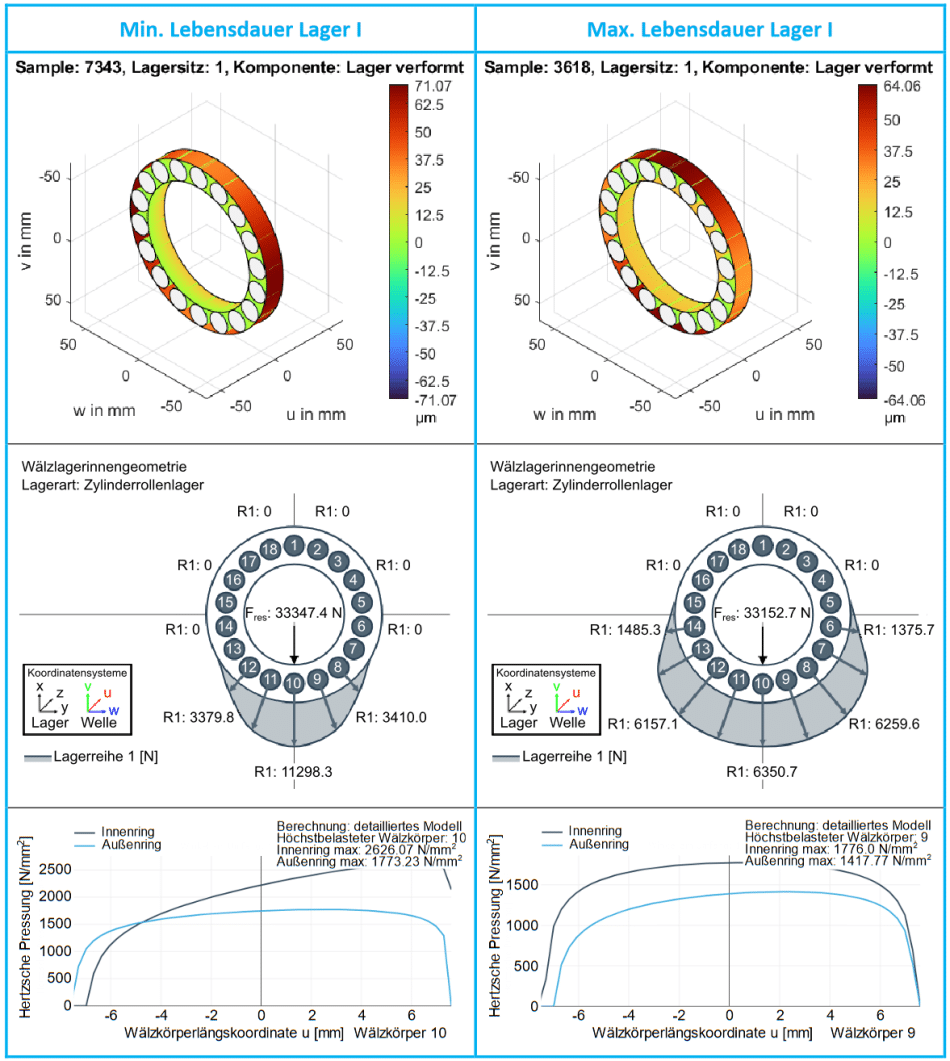
07: Laufbahngeometrie (oben), Wälzkörperlastaufteilung (mittig) und axialer Pressungsverlauf am höchstbelasteten Wälzkörper (unten) bei minimaler (links) bzw. maximaler (rechts) Lebensdauer Lnmrh am Lager I
4 Zusammenfassung
Anhand des im Beitrag vorgestellten Beispiels wird deutlich, dass Geometrieabweichungen der Lagerlaufbahnen einen erheblichen Einfluss auf wesentliche Eigenschaften von Wälzlagern wie die hier betrachtete Lebensdauer haben. In der Praxis können diese z. B. aus der Deformation der Lagerringe bei der Montage infolge nicht ideal zylindrischer Lagersitzgeometrien herrühren. Der Effekt ist abhängig von deren Art und Größe sowie den vorliegenden Betriebsbedingungen. Er ist jedoch nicht zwingend negativ und kann im Gegenteil sogar deutlich positiv ausfallen. Die FVA-Workbench bietet Anwenderinnen und Anwendern die Möglichkeit, geometrische Abweichungen bei der Lagerauslegung direkt zu berücksichtigen. Über die integrierte Skripting-Schnittstelle besteht dabei die Option, benutzerdefinierte Berechnungsroutinen (z. B. die Einbindung von durch FE-Berechnung ermittelten Ringverformungen oder statistische Toleranzanalysen) mit geringem Aufwand umzusetzen.
Autoren:
Vincent Kramer, M. Sc.
Lehrstuhl für Konstruktionstechnik,
Friedrich-Alexander-Universität Erlangen-Nürnberg,
Deutschland
Dr.-Ing. Marcel Bartz
Lehrstuhl für Konstruktionstechnik,
Friedrich-Alexander-Universität Erlangen-Nürnberg,
Deutschland
Dr.-Ing. Stefan Götz
Lehrstuhl für Konstruktionstechnik,
Friedrich-Alexander-Universität Erlangen-Nürnberg,
Deutschland
Prof. Dr.-Ing. Benjamin Schleich
Product Life Cycle Management,
Technische Universität Darmstadt,
Deutschland
Prof. Dr.-Ing. Sandro Wartzack
Lehrstuhl für Konstruktionstechnik,
Friedrich-Alexander-Universität Erlangen-Nürnberg,
Deutschland
Literaturverzeichnis
[1] DIN 26281: Wälzlager – Dynamische Tragzahlen und nominelle Lebensdauer-Berechnung der modifizierten nominellen Referenz-Lebensdauer für Wälzlager. Beuth Verlag, Berlin, 2010
[2] Schleich, B: Skin Model Shapes: A new Paradigm for the Tolerance Analysis and the Geometrical Variations Modelling in Mechanical Engineering. Dissertation Friedrich-Alexander-Universität Erlangen-Nürnberg, 2017
[3] Fingerle, A.; Hochrein, J. et al.: Theoretical Study on the Influence of Planet Gear Rim Thickness and Bearing Clearance on Calculated Bearing Life. Journal of Mechanical Design, 142 (2020) 3, Art. Nr. 031102
[4] FVA Workbench: https://www.fva-service.de/de/software/
[5] Guyan, R.: Reduction of Stiffness and Mass Matrices. AIAA Journal, 3 (1965), S. 380-380
[6] Dokumentation FVA Workbench Scripting Schnitt-stelle: https://doc.fva-service.de/80/de/scripting.html
[7] DIN 620-4: Wälzlager – Wälzlagertoleranzen – Teil 4: Radiale Lagerluft. Beuth Verlag, Berlin, 2004
[8] Siebertz, K.; van Bebber, D.; Hochkirchen, T.: Statistische Versuchsplanung. Design of Experi-ments (DoE). Springer Verlag, Berlin, Heidelberg, 2017
[9] Teutsch, R.; Sauer, B.: An Alternative Slicing Technique to Consider Pressure Concentrations in Non-Hertzian Line Contacts. Journal of Tribology, 126 (2004), 3, S. 436-442
Text- und Bildquelle: FVA und die Autoren